Pascal
Pascal se caracteriza por ser un lenguaje de programación estructurado fuertemente tipificado. Esto implica que:
El código está dividido en porciones fácilmente legibles llamadas funciones o procedimientos. De esta forma Pascal facilita la utilización de la programación estructurada en oposición al antiguo estilo de programación monolítica.
El tipo de dato de todas las variables debe ser declarado previamente para que su uso quede habilitado.
El nombre de Pascal fue escogido en honor al matemático Blaise Pascal.
Diferencias
Además sus programas tienen definidas dos partes: declarativa y ejecutiva. En la primera debe aparecer todo lo que se usará en la segunda, de lo contrario se detecta como desconocido y evita ciertas incomprensiones como veremos más adelante. En la parte declarativa se enuncian Unit existentes, procedimientos, funciones, variables, constantes y nuevos tipos de datos estructurados.
Otra diferencia importante es que en Pascal, el tipo de una variable se fija en su definición; la asignación a variables de valores de tipo incompatible no están autorizadas (en C, en cambio, el compilador hace el mejor esfuerzo para dar una interpretación a casi todo tipo de asignaciones). Esto previene errores comunes donde variables son usadas incorrectamente porque el tipo es desconocido; y también evita la necesidad de notaciòn Hungara, que vienen a ser prefijos que se añaden a los nombres de las variables y que indican su tipo.
Copiladores
Epox
Compilador GNU Pascal (GPC), escrito en C, basado en GNuCompiler Collection (GCC). Se distribuye bajo licencia GLP.
Free Pascal está escrito en Pascal (el compilador está creado usando Free Pascal), es un compilador estable y potente. También distribuido libremente bajo la licencia GPL. Este sistema permite mezclar código Turbo Pascal con código Delphi, y soporta muchas plataformas y sistemas operativos.
Turbo pascal fue el compilador Pascal dominante para PC durante los años 1980 y hasta principios de los años 1990, muy popular debido a sus magníficas extensiones y tiempos de compilación sumamente cortos. Actualmente, versiones viejas de Turbo Pascal (hasta la 7.0) están disponibles para descargarlo gratuito desde el sitio de Borland (es necesario registrarse).
Delphi es un producto tipo RAD (Rapid Application Development) de Borland. Utiliza el lenguaje de programación Delphi, descendiente de Pascal, para crear aplicaciones para la plataforma Windows. Las últimas versiones soportan compilación en la plataforma .NET.
Kylis es la versión más nueva de Borland reiterando la rama de Pascal de sus productos. Es descendiente de Delphi, con soporte para el sistema operativo Linux y una librería de objetos mejorada (CLX). El compilador y el IDE están disponibles para uso no comercial. Actualmente este proyecto está descontinuado.
Lazarus es un clon de Delphi, basado en Free pascal es software libre.
Midlet Pascal para la plataforma J2ME.
TMT. Pascal.
Turbo Pascal
Ejemplo 1: Algunos ejemplos son:
111 + 6 (operación suma)
19 - 72 (operación resta)
24 * 3 (operación multiplicación)
Todas las operaciones del ejemplo constan de dos operandos (constantes enteras) y un operador. La mayoría de las veces es así, pero, también es posible realizar operaciones con distinto número de operadores y/u operandos.
Ejemplo 2: Por ejemplo:
111 + 6 - 8 (tres operandos y dos operadores) -( ( +19 ) + 72 ) (dos operandos y tres operadores) -( -72 ) (un operando y dos operadores)
En las operaciones del ejemplo se puede observar que los caracteres más (+) y menos (-) tienen dos usos:
1. Operadores suma y resta.2. Signos de un número (también son operadores).
Los operadores de signo más (+) y menos (-) son operadores monarios, también llamados unarios, ya que, actúan, solamente, sobre un operando.Los caracteres abrir paréntesis "(" y cerrar paréntesis ")" se utilizan para establecer la prioridad de los operadores, es decir, para establecer el orden en el que los operadores actúan sobre los operandos.Un operador indica el tipo de operación a realizar sobre los operandos (datos) que actúa. Los operandos pueden ser:
Constantes (expresadas por su valor o con un nombre (identificador)).
Variables.
Llamadas a funciones.
Elementos de formaciones (arrays).
En este apartado se van a tratar operaciones en donde sólo aparecen constantes y variables. Cuando se combinan uno o más operadores con uno o más operandos se obtiene una expresión. De modo que, una expresión es una secuencia de operandos y operadores escrita bajo unas reglas de sintaxis.
Ejemplo 3: Dadas las siguientes declaraciones de constantes y variables:
const PI = 3.141592; var Numero : Integer; Radio_circulo : Real;Algunos ejemplos de expresiones son: 2 * PI * Radio_circulo ( PI * PI ) Numero * 5
El valor de la constante PI viene dado en su declaración (3.141592). No obstante, los valores de las variables Numero y Radio_circulo serán dados en la ejecución del programa. Por ejemplo, podrían asignarse mediante dos instrucciones de asignación en el bloque de instrucciones principal del programa:
begin
...
Numero := 2; Radio_circulo := 3.2;
...
end.
Nota: Fíjese que, en Pascal, la sintaxis para realizar una instrucción de asignación es:
Por tanto, al evaluar las expresiones del ejemplo 3, se obtendrían los valores: 20.106189 (valor real) ( 2 * 3.141592 * 3.2 ) 9.869600 (valor real) ( 3.141592 * 3.141592 ) 10 (valor entero) ( 2 * 5 )Un operador siempre forma parte de una expresión, en la cual, el operador siempre actúa sobre al menos un operando. Por el contrario, un operando sí puede aparecer solo en una expresión.En programación, de la evaluación de una expresión siempre se obtiene un valor. Dicho valor puede ser de tipo: entero, real, lógico, carácter o cadena. Por consiguiente, una expresión puede ser:
Aritmética (devuelve un número entero o real).
Lógica (devuelve un valor lógico: verdadero o falso)
De carácter (devuelve un carácter representable por el ordenador).
De cadena (devuelve una cadena).
A continuación, vamos a estudiar los operadores y las expresiones en Turbo Pascal.
Expresiones aritméticasDe la evaluación de una expresión aritmética siempre se obtiene un valor de tipo entero o real. En las expresiones aritméticas se pueden utilizar los siguientes operadores aritméticos:
Operadores Aritméticos en Turbo Pascal:
+ Suma - Resta * Multiplicación / División real div División entera mod Módulo (resto de la división entera) + Signo más - Signo menos
Figura. Clasificación de los operadores aritméticos en Turbo Pascal.
Ejemplo 4: El operador multiplicación (*) realiza la multiplicación de dos operandos numéricos. 5 * 2 3.1 * 2.5
Los resultados son: 10 (valor entero) 7.75 (valor real)
Ejemplo 5: El operador división real (/) realiza la división real entre dos operandos numéricos. 5 / 2 3.1 / 2.5 6 / 2
Sus resultados son:
2.5 (valor real) 1.24 (valor real) 3.0 (valor real)
Ejemplo 6: El operador división entera (div) realiza la división entera entre dos operandos numéricos enteros. 5 div 2 3.1 div 2.5
El operador división entera (div) no puede operar con operandos numéricos reales. Por tanto, al evaluar las expresiones de este ejemplo se obtienen los valores:
2 (valor entero) ERROR (no se puede evaluar; ambos operandos deben ser valores enteros)
Ejemplo 7: El operador módulo (mod) realiza la división entera entre dos operandos numéricos enteros, devolviendo el resto de la misma. 5 mod 2 3.1 mod 2.5
Al igual que el operador división entera (div), el operador módulo (mod) tampoco puede operar con operandos numéricos reales.
De modo que, en este caso, los resultados son:
1 (valor entero) ERROR (no se puede evaluar; ambos operandos deben ser valores enteros)
Ejemplo 8: El operador signo menos (-) cambia el signo de un operando numérico. Así, de las expresiones -11 -( 3.1 ) -( -2.5 )se obtienen los valores:
-11 (valor entero)
-3.1 (valor real)
2.5 (valor real)
Prioridad de los operadores aritméticos.
Ejemplo 9: En una expresión aritmética puede aparecer más de un operador aritmético.
11 + 3 div 3 (dos operadores)
-3 * 6 mod 4 (tres operadores)
-3.1 + 5 * 0.5 (tres operadores)
+3 * -8 (tres operadores)
Para poder evaluar correctamente las expresiones aritméticas del ejemplo, es necesario seguir un criterio de prioridad de operadores. En Turbo Pascal, la prioridad de los operadores aritméticos es:
Prioridad de los operadores aritméticos (de mayor a menor) en Turbo Pascal:
* / div mod Multiplicación, división real, división entera y módulo
+ - Suma (o Signo más) y resta (o Signo menos)
(Figura. Prioridad de los operadores aritméticos en Turbo Pascal.)
Todos los operadores aritméticos con la misma prioridad, por ejemplo, el operador multiplicación (*) y el operador módulo (mod), se evalúan de izquierda a derecha. En consecuencia, los valores que proporcionan las expresiones del ejemplo 9 son: 12 (actúan en orden los operadores: (div) y suma (+)) -2 (actúan en orden los operadores: (*), (mod) y signo menos (-)) -0.6 (actúan en orden los operadores: (*), signo menos (-), y suma (+)) -24 (actúan en orden los operadores: (*), signo menos (+) y signo menos (-))Para modificar la prioridad de los operadores en las expresiones, se debe hacer uso de los caracteres abrir paréntesis "(" y cerrar paréntesis ")".En las expresiones aritméticas hay que tener la precaución de no dividir entre cero (0).
Ejemplo 10: Por tanto, las siguientes expresiones son incorrectas:
11 / 0
5 div 0
-3 mod 0
De la evaluación de cada una de estas expresiones se obtiene: ERROR (no se puede evaluar; no se puede dividir entre cero)
Expresiones lógicas
De la evaluación de una expresión lógica siempre se obtiene un valor de tipo lógico (TRUE o FALSE). En las expresiones lógicas se pueden utilizar dos tipos de operadores:
· Relacionales
· Lógicos
Un operador relacional se utiliza para comparar los valores de dos expresiones. Estas deben ser del mismo tipo (aritméticas, lógicas, de carácter o de cadena).
Ejemplo 11: Algunos ejemplos son:
22 > 13 (comparación de dos expresiones aritméticas)
22.5 < 3.44 (comparación de dos expresiones aritméticas) TRUE = FALSE (comparación de dos expresiones lógicas)
'c' > 'f' (comparación de dos expresiones de carácter)
"coche" = "Coche" (comparación de dos expresiones de cadena)
Proporcionan los valores:
TRUE (22 es mayor que 13)
FALSE (22.5 no es menor que 3.44)
FALSE (TRUE no es igual que FALSE)
FALSE ('c' no es mayor que 'f')
FALSE ("coche" no es igual que "Coche")
Las comparaciones entre los valores de tipo numérico son obvias. En cuanto a los valores de tipo lógico (TRUE y FALSE) se considera que FALSE es menor que TRUE. En lo que respecta a los valores de tipo carácter, su orden viene dado por el ASCII extendido utilizado por el ordenador para representarlos. Y en el caso de los valores de tipo cadena, también se tiene en cuenta dicho código.
Los operadores relacionales son:
Operadores Relacionales en Turbo Pascal:
< Menor que <= Menor o igual que > Mayor que >= Mayor o igual que = Igual que <> Distinto que
(Figura. Clasificación de los operadores relacionales en Turbo Pascal.)
Nota: Existe un operador relacional más (in), del cual hablaremos más adelante.Para escribir una expresión relacional (lógica) se utiliza la sintaxis:
Siendo
Por otra parte, un operador lógico actúa, exclusivamente, sobre valores de expresiones lógicas.
Los operadores lógicos son:
Operadores Lógicos en Turbo Pascal:
and Conjunción
or Disyunción
not Negación
(Figura. Clasificación de los operadores lógicos en Turbo Pascal.)
Nota: Existen tres operadores lógicos más (xor, shl y shr ), de los cuales hablaremos más adelante.
El operador conjunción (and) y el operador disyunción (or) siempre actúan sobre dos operandos, mientras que, el operador negación (not) sólo actúa sobre un operando, o dicho de otra forma, es un operador monario.
El modo en que actúan los operadores lógicos se resume en las llamadas tablas de verdad, definidas por el matemático George Boole.La tabla de verdad del operador conjunción (and) es:
TRUE
TRUE
FALSE
FALSE
TRUE
FALSE
TRUE
FALSE
TRUE
FALSE
FALSE
FALSE
(Figura. Tabla de verdad del operador conjunción (and) en Turbo Pascal.)
Se supone que
Ejemplo 12:
Algunos ejemplos son:
( 9 > 3 ) and ( 8 > 6 )
( 9 > 3 ) and ( 8 > 9 )
( 9 = 3 ) and ( 8 >= 6 )
( 9 = 3 ) and ( 8 >= 9 )
Las expresiones anteriores se evalúan a:
TRUE (9 > 3 es TRUE y 8 > 6 es TRUE)
FALSE (9 > 3 es TRUE y 8 > 9 es FALSE)
FALSE (9 = 3 es FALSE y 8 >= 6 es TRUE)
FALSE (9 = 3 es FALSE y 8 >= 9 es FALSE)
La tabla de verdad del operador disyunción (or) es:
TRUE
TRUE
FALSE
FALSE
TRUE
FALSE
TRUE
FALSE
TRUE
TRUE
FALSE
TRUE
(Figura. Tabla de verdad del operador disyución (or) en Turbo Pascal.)
De la tabla de verdad se deduce que si al menos una de las dos expresiones es verdadera, el resultado será TRUE.
La tabla de verdad del operador negación (not) es:
TRUE
FALSE
not
FALSE
TRUE
Figura. Tabla de verdad del operador negación (not) en Turbo Pascal.
El valor de not
Ejemplo 13: De las expresiones
not ( 9 > 3 )
not ( 8 > 9 )
los resultados de evaluarlas son:
FALSE (9 > 3 es TRUE)
TRUE (8 > 9 es FALSE)
Prioridad de los operadores relacionales y lógicos
En una expresión lógica puede aparecer uno o más operadores relacionales y/o lógicos.
Ejemplo 14: Algunos ejemplos son:
( 3 > 1 ) or ( 4 < 1 ) and ( 4 <= 2 )
not FALSE and FALSE
Para poder evaluar correctamente las expresiones lógicas del ejemplo, es necesario seguir un criterio de prioridad de operadores. En Turbo Pascal, la prioridad entre los operadores relacionales y lógicos es:
Prioridad de los operadores relacionales y lógicos (de mayor a menor) en Turbo Pascal:
not Negación
and shl shr Conjunción, Desplazamiento a la izquierda y Desplazamiento a la derecha
or xor Disyunción y OR exclusiva
< <= > >= = <> in Menor que, Menor o igual que, Mayor que, Mayor o igual que, Igual que, Distinto que y En
(Figura. Prioridad de los operadores relacionales y lógicos en Turbo Pascal.)
Los operadores con la misma prioridad, por ejemplo, el operador menor que (<) y el operador mayor que (>), se evalúan de izquierda a derecha. Así que, los valores que proporcionan las expresiones del ejemplo 14 son:
TRUE (actúan en orden los operadores: (>), (<), (<=), (and) y (or))
FALSE (actúan en orden los operadores: (not) y (and))
Expresiones de carácter
Aunque no existe ningún operador de caracteres, sí que existen expresiones de carácter. De la evaluación de una expresión de carácter siempre se obtiene un valor de tipo carácter.
Ejemplo 15: Dadas las siguientes declaraciones de constantes y variables en Turbo Pascal:
const
CONSONANTE = 'S';
var
Letra, Opcion : Char;
y realizadas las siguientes asignaciones:
begin
...
Letra := 'X';
Opcion := '3';
...
end.
Algunas expresiones de carácter son:
Opcion
Letra
CONSONANTE
'a'
Los resultados de evaluarlas son:
'3'
'X'
'S'
'a'
Expresiones de cadena
De la evaluación de una expresión de cadena siempre se obtiene un valor de tipo cadena. En Turbo Pascal sólo existe un operador de cadena:
Operador de Cadena en Turbo Pascal:
+ Concatenación
(Figura. Clasificación de los operadores de cadena en Turbo Pascal.)
El operador concatenación (+) realiza la concatenación de dos operandos de tipo cadena, es decir, los encadena.
Ejemplo 16: Dadas las siguientes declaraciones de constantes y variables en Turbo Pascal:
const
OLIMPIADA = 'Atenas 2004';
PUNTO = '.';
var
Nombre : String [5];
Apellido : String [5];
Rio : String [4];
y realizadas las siguientes asignaciones:
begin
...
Nombre := 'Pedro';
Apellido := 'Cosín';
Rio := 'Tajo';
...
end.
Algunas expresiones de cadena son:
OLIMPIADA + PUNTO
Nombre + ' ' + Apellido
'Buenos días' + PUNTO
Rio
Nombre + ' fue a las Olimpiadas de ' + OLIMPIADA +PUNTO
Los resultados de evaluarlas son:
'Atenas 2004.'
'Pedro Cosín'
'Buenos días.'
'Tajo'
'Pedro fue a las Olimpiadas de Atenas 2004.'
Prioridad de los operadores aritméticos, relacionales, lógicos y de cadena
En una expresión puede aparecer uno o más operadores aritméticos, relacionales, lógicos y/o de cadena.
Ejemplo 17: Algunos ejemplos son:
( 5 * 4 > 5 + 4 ) or FALSE and ( 'ab' < 'aa' )
( ( 5 * 4 > 5 + 4 ) or FALSE ) and ( 'f' < 'b' )
not TRUE < FALSE
not ( TRUE < FALSE )
Para poder evaluar correctamente las expresiones anteriores, es necesario seguir un criterio de prioridad de operadores. En Turbo Pascal, la prioridad entre los operadores aritméticos, relacionales, lógicos y de cadena es:
Prioridad de los operadores aritméticos, relacionales, lógicos,de cadena y puntero (de mayor a menor) en Turbo Pascal:
@ not Puntero y Negación
* / div mod and shl shr Multiplicación, División real, División entera, Módulo y Conjunción
+ - or xor Suma (o Signo más o Concatenación), Resta (o Signo menos), Disyunción y OR exclusiva
< <= > >= = <> in Menor que, Menor o igual que, Mayor que, Mayor o igual que, Igual que, Distinto que y En
Figura. Prioridad de los operadores aritméticos, relacionales, lógicos, de cadena y puntero en Turbo Pascal.
Nota: Fíjese que, en la tabla se ha incluido también el operador puntero (@), el cual se estudiará más adelante. De esta forma, en la tabla, quedan recogidos todos los operadores que existen en Turbo Pascal.
Por tanto, los valores que proporcionan las expresiones del ejemplo 18 son:
TRUE (actúan en orden los operadores: (*), suma (+), (>), (<), (and) y (or))
FALSE (actúan en orden los operadores: (*), suma (+), (>), (or), (<) y (and))
FALSE (actúan en orden los operadores: (not) y (<))
TRUE (actúan en orden los operadores: (<) y (not))
Obsérvese que, los paréntesis "()" son capaces de cambiar el orden de actuación de los operadores de cualquier expresión. Además, los paréntesis se pueden anidar, es decir, se pueden escribir unos dentro de otros, priorizándose del más interno al más externo y, después, de izquierda a derecha.
Ejemplo 18: De la expresión
42 mod ( ( 4 - 5 ) * ( 8 + 2 ) )se obtiene el valor:
2 (actúan en orden los operadores: (-), (+), (*) y (mod).
Triangulo de pascal
El triángulo de Pascal se construye de la siguiente manera: se comienza en el número «1» centrado en la parte superior; después se escriben una serie de números en las casillas situadas en sentido diagonal descendente, a ambos lados, del siguiente modo: se suman las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) se escribe debajo de dichas casillas; el proceso continúa escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3)...
La construcción del triángulo está relacionada con los coeficientes binomiales según la fórmula (también llamada Regla de Pascal):
Si 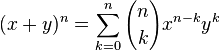
entonces 
para todo entero positivo n y todo entero positivo k entre 0 y n.
Las cifras escritas en cada fila del triángulo, corresponden a los coeficientes del desarrollo binomial:


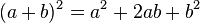

No hay comentarios:
Publicar un comentario